Feature transformation involves modifying data while keeping the information to give them more discriminatory power. The new data may have different interpretation from the original data. Key feature transformation methods are outlined below.
Numeric Data #
Binning or bucketing converts numeric features into categorical type normally to reduce cardinality, e.g., converting income figures into categories “low”, “medium”, and “high”, or converting values of transactions in an eCommerce shop into 50 bins only. Popular approaches are equal-width binning, equal-frequency binning and entropy-based binning.
Numeric to binary is a special case of binning with only 2 bins – true or false, e.g. a class mark less than 50% is encoded as “fail” and a mark 50% or above is encoded “pass”
Scaling enlarges or diminishes values of features that have very different scales or units to a specific range (e.g., 50 to 100) in order to eliminate the dominance of some features over others; e.g., slight changes in “house price” will dominate results for a dataset that contains “house price” stated in hundreds of thousands of dollars and “number of rooms”. Scaling is required by algorithms such as k-means and k-nearest neighbors that work by calculating the distance between the data points. Common methods are min-max scaling, mean scaling and standardization (Z-score).
Categorical Data #
Categorical values must be converted to numbers because many machine learning algorithms accept only numbers as input.
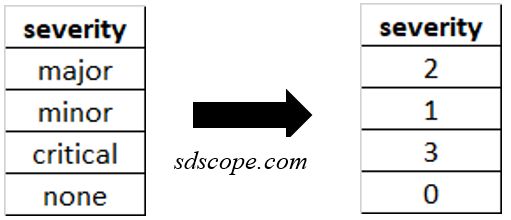
Label encoding assigns a different integer to each unique value for ordinal features. See Figure 1.
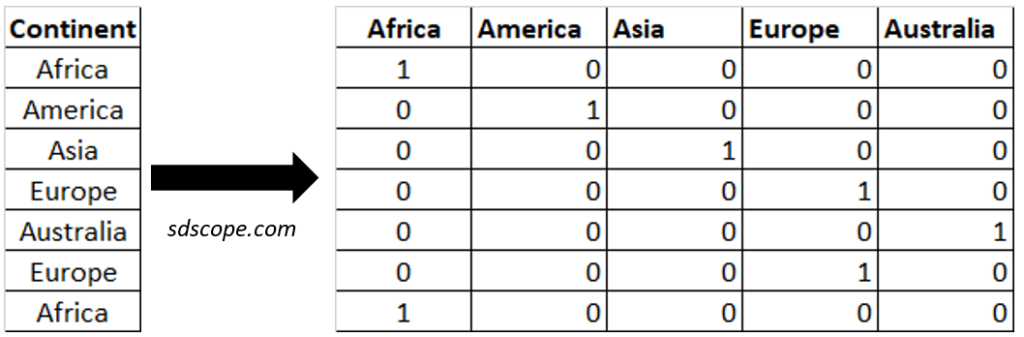
One-hot-encoding creates a new column for each possible value of a categorical feature and maps the value to 1 or 0 depending on the presence of the value. This is useful for nominal features (where there is no intrinsic ranking or order), Figure 2.
Flagging replaces a value by a 0/1 flag indicating presence or absence. It equally applies to mapping binary values.
Functional Transformation #
Functional transformation changes the underlying shape of data to fulfill the assumptions of certain algorithms or to enable better visualization, e.g., log transformation to make quadratic distributions more linear to enable separation of classes.
Normalization is the most popular method of functional transformation that transforms data in a feature so that its distribution is normal/ bell curve /Gausian (i.e., remove skewness, linearity or heteroskedasticity) in order to meet the requirements of algorithms such as linear discriminant analysis that assume data is normally distributed. Normalization preserves impact of outliers. Common transformations are log, square root and inverse.
Other Transformations #
Date to numeric transformation extracts components from date or time as numeric values relative to other components; e.g., hour relative to day, hour relative to month, or day relative to year
Text processing encodes text data in a way which is ready to be used by machine learning algorithms e.g., in sentiment analysis. Examples of such encoding are TFIDF vectorization and tokenization.




